Kinetyka reakcji

Szybkość reakcji

Równanie kinetyczne opisuje zależność między chwilową szybkością reakcji a stężeniami reagentów. Ma ono postać:

\[ v = k \cdot [A]^{x} \cdot [B]^{y} \]

gdzie [A] oraz [B] to stężenia molowe substratów. Wielkość k jest nazywana stałą szybkości reakcji.

Na podstawie równania kinetycznego można przewidzieć, jak będzie zmieniać się szybkość reakcji po zmianie warunków tej reakcji.

Przykład 1

Dana jest reakcja tworzenia tlenku azotu z następujących składników: \[ 2 NO + O_{2} \rightarrow 2 NO_{2} \] Na tej podstawie napisz równanie kinetyczne oraz określ jej rzędowość. Czy zawsze można napisać równanie kinetyczne mając dane równanie reakcji procesu?

1. Zaczynamy od równania kinetycznego. \[ v = k \cdot [NO]^{2} \cdot [O_{2}] \]
2. Określamy rzędowość reakcji. Sumujemy wykładniki potęg w równaniu kinetycznym i widzimy, że podana reakcja jest III rzędu.
3. Równanie kinetyczne ustala się ostatecznie zawsze doświadczalnie. Złożone, wieloetapowe reakcje nie dają się tak łatwo zapisać i ich równanie kinetyczne często ma inną postać, niż sugerowałoby to sumaryczne równanie reakcji.
4. Odpowiedź: reakcja jest III rzędu.

Przykład 2

Szybkość reakcji hydrolizy sacharozy jest dana następującym równaniem kinetycznym: \[ v = k \cdot [C_{12}H_{22}O_{11}] \cdot [H^{+}] \] Oblicz, jak zmieni się szybkość reakcji, jeżeli stężenie cukru wzrośnie dwukrotnie, a stężenie jonów wodorowych wzrośnie czterokrotnie.

1. Zaczynamy od zapisania równania kinetycznego na szybkość początkową pierwszego układu. \[ v_{1} = k \cdot [C_{12}H_{22}O_{11}] \cdot [H^{+}] \]
2. Zapisujemy analogiczne równanie dla stężeń po zmianie warunków: \[ v_{2} = k \cdot 2[C_{12}H_{22}O_{11}] \cdot 4[H^{+}] \]
3. Przyrównujemy obie szybkości reakcji. \[ \frac{v_{2}}{v_{1}} = \frac{k \cdot 2[C_{12}H_{22}O_{11}] \cdot 4[H^{+}]}{k \cdot [C_{12}H_{22}O_{11}] \cdot [H^{+}]} = 8 \]
4. Odpowiedź: Szybkość reakcji wzrośnie ośmiokrotnie.

Reakcja I rzędu

Reakcje pierwszego rzędu to takie, których szybkość zależy tylko od stężenia jednego substratu i to w pierwszej potędze. Takimi reakcjami są reakcje samoistnego rozpadu molekuł lub zmiany ich konfiguracji (np. jak to ma miejsce w cząsteczce amoniaku, która składa się jak parasol pod wpływem silnego wiatru). Najbardziej sztandarowym przykładem reakcji I rzędu są jednak rozpady promieniotwórcze. W ich wypadku stężenie substratu można śmiało zastąpić masą materiału promieniotwórczego.

Przy tych reakcjach można się posłużyć równaniem kinetycznym zapisanym w następujący sposób:

\[ ln\frac{C_{0}}{C} = k \cdot t\\ [C] = [C_{0}] \cdot e^{-k\cdot t}\\ ln[C] = ln[C_{0}] - k \cdot t\\ k = \frac{ln2}{t_{1/2}} \]

gdzie t_½ to czas połowicznego rozpadu, czyli czas, po którym zanika połowa materiału promieniotwórczego. Jest to wielkość charakterystyczna dla danej substancji.

Przykład 3

Oblicz masę promieniotwórczego izotopu, jaki pozostał po tygodniu przechowywania próbki o masie 12 g, jeżeli jej czas połowicznego rozpadu wynosi 3 dni.

1. Zaczynamy od obliczenia stałej szybkości reakcji. \[ k = \frac{ln2}{3\;dni} = 0,231 \frac{1}{dzień} \]
2. Rozpisujemy odpowiednią zależność i obliczamy. \[ [m] = [m_{0}] \cdot e^{-k\cdot t}\\ [m] = 12 \cdot e^{- 0,231 \frac{1}{dzień} \cdot 7 \; dni}\\ m = 2,38 g \]
3. Odpowiedź: po tygodniu pozostanie 2,38 g próbki.

Przykład 4

Na podstawie wykresu oszacuj masę promieniotwórczego izotopu, jaki pozostał po tygodniu przechowywania próbki o masie 12 g, jeżeli czas połowicznego rozpadu wynosił 3 dni.

1. Zaczynamy od przygotowania tabeli zależności masy próbki od czasu przechowywania.

   Czas przechowywania [dni]	0	3	6	9	12
   Masa pozostałego izotopu [g]	12	6	3	1,5	0,75

2. Następnie rysujemy odpowiedni wykres.
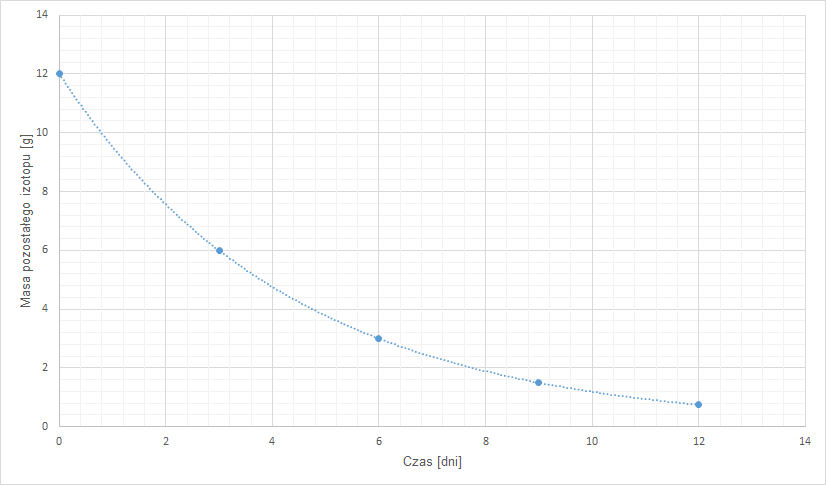
3. Odczytujemy z wykresu masę.
4. Odpowiedź: po tygodniu pozostanie około 2,5 g próbki.